阿部さんの輪読会 http://swikis.ddo.jp/abee/10 であったように、シーモア・パパートの『マインドストーム』のまえがきにこう書いてあります。
歯車は、群や相対運動などという優れた高等数学の概念を説明するのにも用いることが出来るが、それ以上の効果もある。
これは歯車ファンの私にとっては放っておけません。はて、歯車と群が関係あるとはどういう事だろう。大体群って何だろうか?グーグルで探すと次の定義 http://www.suriken.com/knowledge/glossary/group.html が見つかりました。
空でない集合 G の任意の2つの 元 a,b に対して、 1つの演算・が定義されていて、つぎの条件を満たすとき、G は演算・に関して群をなすという。
なんかむずかしい。。。ゆっくりいきましょう。まず群で使う演算と要素を決めないといけませんが、歯車は歯がいっぱいで描くのがややこしいし、噛み合わせると逆回転してトリッキーなので、滑車で考えます。まず手始めに、直径 1 センチの滑車を用意してヒモを掛け、動きを見ます。
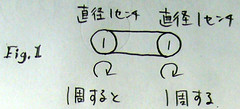
Fig.1 のように、左の滑車を一周回すと、右の滑車も一周回ります。これから、繋げた滑車の一番左を一周すると残りは何周するかというのを考えましょう。
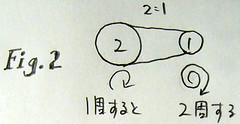
次の Fig.2 は左右の滑車の大きさが違う場合です。左が直径 2 センチで右が 1 センチの時、左を 1 周すると右は 2 周します。この組み合わせを文字で書く時は 2:1 のように書きましょう。このように滑車とヒモの一組をわたし達の群で使う要素と考えます。
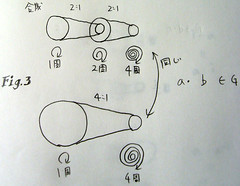
要素が決まったので演算・について考えます。2:1 の滑車を二個繋げたらどうなるでしょうか?Fig.3 のように軸を合わせて繋げると、4:1 の大きな滑車一組と同じ意味になって、左を一周すると一番右は四周します。式で書くと、2:1 ・ 2:1 = 4:1 のようにします。繋げた滑車も一組の滑車と同じように動くというのが、条件 1 の演算・について閉じているという意味です。
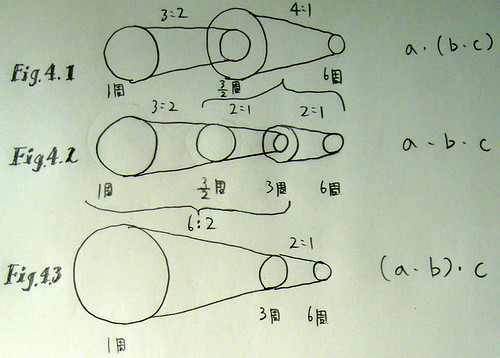
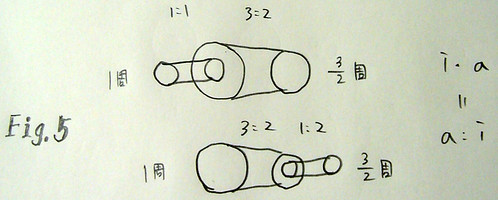
では、滑車の組を三つ繋げたらどうなるでしょうか(Fig. 4.2)?三つの時も、一つと二つの組み合わせと考えると良いです。例えば、3:1 ・ 2:1 ・ 2:1 は二通りの考え方が出来ます。
- 3:2 ・ 2:1 ・ 2:1 = 3:2 ・ (2:1 ・ 2:1) = 3:2 ・ 4:1 = 12 : 2 (Fig. 4.1)
- 3:2 ・ 2:1 ・ 2:1 = (3:2 ・ 2:1) ・ 2:1 = 6:2 ・ 2:1 = 12 : 2 (Fig. 4.3)
このように、三つの要素を組み合わせる時に組み合わせる優先度を問わない事を条件 2 の結合法則と言います。
滑車の組み合わせを考える時に、一つ覚えておくと便利なやつがあります。最初に挙げた 1:1 の滑車は、左を回しただけきっちり同じ回数右を回します。こういう滑車は他のやつと組み合わせても性質を変えないのでの単位元と言います(条件 3)。条件では、単位元は一つしかない事になっていますが、わたし達の滑車では 2:2 も 3:3 も単位元になってしまうので、このように同じ動きをする滑車の組は「同じ」という決まりにすれば良いと思います。
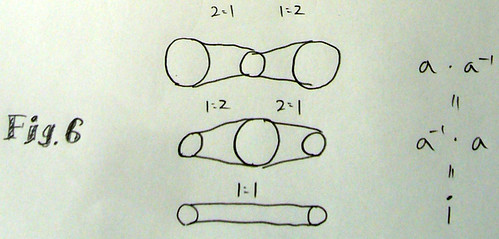
滑車を組み合わせて単位元を作る事も出来ます。例えば、2:1 の滑車があるとき、さらに 2:1 を繋げると全体として 1:1 と同じ意味になります。逆に、1:2 に 2:1 を組み合わせても同じです。このように、組み合わせると単位元になるやつを逆元と呼びます(条件 4)。これで条件 1 から条件 4 まで満たす事が分かったので、滑車の組み合わせは群だと考える事が出来ます。
今まで図を書いて考えてきましたが、実はわざわざ図を書かなくても何周するか分かる方法があります。それは歯車の組 1:2 を分数 1/2 として考え、演算・をかけ算×として考えれば良かったのでした。かけ算も代表的な群の一種です。
パパートが言ってるのがこういう事なのかどうか分かりませんが、とりあえず滑車を群として考える例を挙げてみました。ところで差動歯車のビデオめっちゃかっこいいですね! http://www.youtube.com/watch?v=F40ZBDAG8-o