Chris Okasaki の Purely Functional Data Structures という本を買ってみました。これは、副作用を使わないでいろいろなデータ構造のアルゴリズムを実装するという大変面白い本で、これを読むと、副作用無しで○○が出来るわけがない!という時の○○がだいぶ減ると思います。
サンプルは Standard ML で書かれているのですが、良くわからないのでHaskell で書き直しながら読んでみます(巻末に Haskell での実装例が載ってるけど見ないふり)。
17 ページに Heap というコレクションが紹介されています。これは次の性質をもったコレクションです。
- 要素は大小関係を持つオブジェクト。
- 最小の要素だけを取り出す事が出来る。
ようするにあるリストをソートして最小の奴を取り出したいという場合、取り出す物が最小の物だけならばソートするより効率の良い方法があるというのが味噌です。
Heap にも色々ありますが、Lestist Heap は次の性質を持つ木で表現されます。
- 木の親要素が持つ値は、子要素が持つ値より必ず小さい。子同士の大小はどうでも良い
- 二つの木をマージする時、左右程よくバランスを取る。要素の追加も木をマージするのと同じ考え。
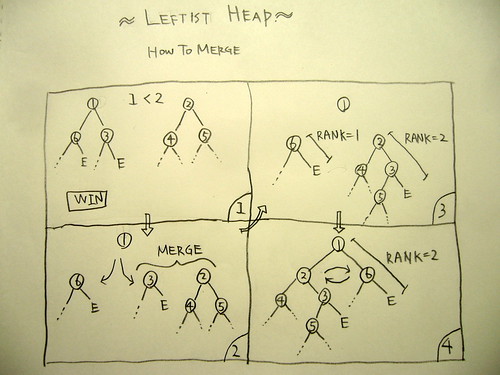
この左右程よくマージするのがポイントなので詳しく書きます。
- まず二つの木の親同士を比べる。小さい方の勝ち。
- 勝った木の親要素が新しい親要素になる。勝った木の右の枝と、負けた木を再起的にマージする。
- ランクを求める。ランクとは、木の右の枝だけを辿って行って空っぽの枝に辿り着くまでのステップ。
- 勝った木と、2 でマージした木のランクを比べて、大きい方を新しい木の左に、小さい方を右に付ける。
この操作で、最大 log2 n のステップでマージ出来ます。ややこしいですが、図をよーく見れば分かると思います。要するに要素を追加する時は右の枝の方に追加するのですが、左が重くなるよう適当に並び替えて行くという具合です。データ構造はこんな感じです。
data Heap a = E | T Int a (Heap a) (Heap a)
ランクを毎度計算するのは大変なので、木に持たせます。木は E (空) か、T ランク 値 左枝 右枝 という形になります。
merge :: Ord a => Heap a -> Heap a -> Heap a merge h E = h merge E h = h merge h1@(T _ x a1 b1) h2@(T _ y a2 b2) | x < y = makeT x a1 (merge b1 h2) | otherwise = makeT y a2 (merge h1 b2)
木のマージはこんな感じ。空の木とのマージは自明です。空でない場合、それぞれの親を比べて、勝者の親要素を親とし、
新しい枝は勝者の左枝と、勝者の右枝と敗者をマージした物になります。makeT で左右の枝の順序と、新しいランクを求めて新しい木を作ります。
rank :: Heap a -> Int rank E = 0 rank (T r _ _ _) = r
ランクのアクセッサです。E の場合はゼロで、それ以外はデータの最初の値です。
makeT :: Ord a => a -> Heap a -> Heap a -> Heap a makeT x a b | rank a >= rank b = T (rank b + 1) x a b | otherwise = T (rank a + 1) x b a
これが肝になる makeT です。ランクを元に左右の順序を決めて、新しい木のランクを決めます。新しい木のランクは必ず右枝のランク + 1 になります。なぜなら、ランクの定義とは、右側だけを辿って行って空に出会うまでのステップで、右枝自体が持つランクに親の分 1 を足したものが新しい木のランクになるからです。
これでだいたい完成。あとはマージの仕組みを応用して色々な機能を付けます。
insert :: Ord a => a -> Heap a -> Heap a insert x h = merge (T 1 x E E) h findMin :: Heap a -> a findMin (T _ x a b) = x deleteMin :: Ord a => Heap a -> Heap a deleteMin (T _ x a b) = merge a b
要素の追加とは、Heap に要素一つの Heap をマージする事です。最小要素へのアクセスは木の親へのアクセス、最小要素の削除は、親の左右の木をマージする事になります。
listToHeap :: Ord a => [a] -> Heap a listToHeap = foldr insert E
リストから Heap の変換を大好きな foldr でやってみました。なんと insert と E を引き数に与えるだけで変換が出来てしまいます。この美しさを語りだすときりが無いのでまた別の機会に書きます。
heapToList :: Ord a => Heap a -> [a] heapToList E = [] heapToList h = findMin h : heapToList (deleteMin h)
Heap から List への変換は、ださいですが再帰を使ってみました。
折角なので、QuickCheck を使ってテストしてみます。とあるリストを Heap に食わせてリストに戻すとソートされているはずだというのをテストします。
prop_Heap :: [Int] -> Bool prop_Heap xs = isSorted (heapToList (listToHeap xs)) isSorted [] = True isSorted (x:[]) = True isSorted (x:y:xs) = x <= y && isSorted (y:xs)
ここで、prop_Heap がテストしたい性質です。isSorted は、要素が全部小さい順になっているか調べる関数です。Test.QuickCheck を import して次のようにやると、QuickCheck が百個適当にテストケースを作って調べてくれます。
*Heap> verboseCheck prop_Heap verboseCheck prop_Heap 0: [-3,1,-1] 1: ... 中略 ... 99: [-8,-4,9,12,-13,-5,-12,-2,-9,0,1,10,12] OK, passed 100 tests.
ソースはこちら: http://gist.github.com/240891